解説：ミニ特集
数理モデルの獲得
気象予報数値モデルと解析予報システム
斉藤 和雄*
*気象庁予報部数値予報課
東京都千代田区大手町 1-3-4
*Numerical Prediction Division, Japan Meteorological
Agency
1-3-4,
Otemachi, Chiyoda-ku, Tokyo, 100-8122, Japan
*E-mail: ksaito@npd.kishou.go.jp
１．はじめに
気象予報は数理モデルの応用対象として最も早くから着目されてきた分野の一つである。電子計算機の黎明期にあたる1950年には米国で数値計算により大気状態を予測する試みが始まり、日本でも1959年に気象予報数値モデルの業務運用が始まっている。気象予報のための数値モデルは、物理法則に基づいて将来の大気状態を定量的に予測するという意味で、他の計算流体力学モデルと共通点を持っているが、地球全体に及ぶ領域を予報対象にすること、水の相変化・放射・地表面過程など、様々な物理過程を含むという意味で特殊なものになっている。また気象予報では、観測データに基づいて大気状態を解析し、正確な初期値を作成することが非常に重要で、最近では初期値解析にも変分法など数学的な手法に基づいた数理モデルが使われるようになってきている。ここでは、数理モデルとしての視点から見た気象予報のための数値モデルの特徴、気象庁の数値解析予報システムについて紹介する。
２．気象予報のための数値モデル
気象分野では数理モデルによる気象予報を数値予報と呼ぶ。数値予報は、物理法則に基づいて大気の状態の時間変化を定量的に求め、将来の大気の状態を予測するものである。乾燥大気の状態を表す代表的な変数としては、風（速度の３成分u, v, w）、気圧(p)、気温(T)がある。これらに対応する予報方程式としては、３方向の運動（量）方程式、連続の式（気圧の予報式）、熱力学第一法則（温度の式）などがあり、状態方程式（密度ρの診断式）、を加えた６つの式が、基本的な方程式となる。実際の数値予報に用いられるモデルでは、大気中の水の状態を表現する式（水の保存則と相変化の式など）が加わり、また支配方程式はモデルの目的に応じて様々に変形される。放射や地表面過程、乱流などの物理過程をモデルで完全に直接計算することは一般には不可能なので、これらの過程の格子スケールへの影響を取り込むためのパラメタリゼーションが行われる。
数値風洞などの計算流体力学に用いられる工学モデルと気象モデルの大きな違いとして、扱う問題の時間・空間的なスケールの違いがある。一般的な短期の天気予報に用いられる数値予報モデルは、時間スケールとして１時間〜数日、空間スケールとしては鉛直方向に数十ｍ〜数十km、水平方向には数十km〜地球全体（全球）までを予報対象領域とする。鉛直運動に伴う大気の断熱圧縮に伴う温度変化は、雲や降水が生じる重要なファクターとなる。このため、気象モデルでは気温に代えて温位
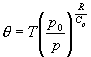
を用いることも多い（Cpは大気の定圧比熱、Ｒは乾燥大気の気体常数、po=1000 hPa）。温位は熱力学第一法則での膨張収縮による仕事に伴う内部エネルギーの変化を考慮した温度で、断熱過程では保存量となる。理想気体の状態方程式には、水蒸気分圧を考慮するために、仮温度を用いる必要がある。水平方向の運動方程式には、地球回転の影響を考慮するためのコリオリ力（転向力）の項や、地球の曲率の影響を考慮するための項が付け加わる。
通常の天気予報に用いられる数値予報モデルでは、現象の鉛直スケールは水平スケールよりも２オーダー程小さいことから、鉛直方向(z)の運動方程式（鉛直加速度と重力、鉛直気圧傾度力の釣り合いの式）を、重力と鉛直気圧傾度力のみの釣り合いの式
に置き換えることが多い（ｇは重力加速度）。上式は静力学の式、あるいは静水圧平衡の式とも呼ばれ、現在の数値予報でよく用いられている近似の一つである。歴史的には、数値予報モデルには大気の大規模運動のみを表現するための近似が基礎方程式系に加えられていたが、概ね1980年代以降では静力学近似以外の近似は行わないモデルが主流になっている。その意味で、静力学近似のみを行う方程式系をプリミティブ方程式系と呼ぶ場合がある。静力学近似を用いないモデル「非静力学モデル」も数値予報に応用され始めており、後章で再度論じる。
他の多くの数理モデルと同様に、数値予報でも場の状態の表現に数値格子を考え格子点の値の時間発展を計算するが、計算効率と計算精度のために様々な工夫がなされている。予報方程式は偏微分方程式の形で書かれるので、差分精度が問題になる場合が多く、それを解決するために多くの数値予報モデルでは水平方向にはスペクトル法[1]を使っている。時間積分には、予報対象とする現象とその他のノイズ（高周波内部重力波など）の時間スケールが違うことに着目して、高周波成分は陰解法するセミインプリシット法[2]や、高周波成分と低周波成分を異なる時間刻みで計算するスプリット法などが使われる。時間積分は、タイムフィルターを併用したリープフロッグ法[3]を用いるものが多いが、近年は移流計算にはセミラグランジアン法[4]を用いるものも多くなっている。これらの詳細については、増田(1981) 1)や時岡ほか(1993)2)などを参考にして頂きたい。通常の気象モデルが予報対象とする現象の時間変化はそれほど急激ではないので、一般には時間方向の差分精度は空間差分の精度に比べて予報結果に与える影響は少ないが、竜巻などの小スケール現象の研究用シミュレーションも想定して高次のルンゲクッタ法などを用いるモデルも現れ始めている。
３．気象庁の数値予報システム
数値予報は、広義には、データの集信から解析・予報、応用プロダクト配信にいたる一連の作業であり、計算機やネットワークなどハードウェアを含めたシステム全体を数値予報システム（あるいは数値解析予報システム）と呼んでいる。気象庁では1959年にIBM704を導入して数値予報業務を始め、以後５〜９年おきに計算機を更新している。現在のシステムは７代目にあたるもので、2001年３月から運用が行われている。中核となるスーパーコンピュータはHitachi SR8000E1（80ノード、768GFLOPS）である。代表的なルーチン運用数値予報モデルとして、表１に示すような、全球・領域・メソの３種のモデルがある。
全球モデル(GSM)は地球全体をカバーするモデルで、明後日予報から週間予報までを主な目的として日に２回運用している。地球全体の大気の流れや降水分布を表現するとともに、領域モデルに境界値を提供するという重要な役割も果たしている。全球の解析は、GSM予報の初期値作成（速報解析）では、データ収集の打ち切り時間[5]は2.5時間であるが、これとは別に打ち切り時間を十分に長く取ってより多くのデータを集めた１日４回の6時間解析予報サイクル（後述）を運用している。
領域モデル(RSM)は、東アジアを計算対象領域とするモデルで、明後日までの短期予報を主な目的として日に２回運用している。現在の気象庁短期予報の中核的支援資料の基になっている。側面境界条件を同じ初期時刻の全球モデルから与えるため、モデルの実行は全球モデルの計算が終わってから始めている。
メソスケールモデル (MSM)は、2001年３月から正式運用が始まったモデルで、約10kmの分解能で日本域とその周辺を計算対象領域としている。防災気象情報の支援を主な目的としており、速報性を重視して短いデータ収集時間で、1日4回の18時間予報を行っている。データ収集の打ち切り時間が早いため、側面境界条件は、同時刻ではなく直前の（６時間ないし12時間前を初期値とする）領域モデルから与えている。
RSMとMSMは計算領域や分解能、初期値・境界値の与え方などは異なるが、モデル本体はほぼ同じものである。GSMとRSM/MSMは、静力学近似を用いるスペクトルモデルであるという点で多くの共通点を持っている。スペクトル展開は、全球モデルでは球面調和関数、領域モデルでは二重フーリエ級数を用いている。鉛直座標系には気圧座標が用いられるが、地表近くでは座標系がモデル地形に沿うように、地表気圧で規格化した気圧σを用いる混成座標が用いられている。全球モデルでは計算の高速化のためにセミラグランジュ法の開発も行なわれている。
表１に掲げたモデルの他に、週間や１ヶ月予報を目的とする全球アンサンブル予報モデルや日本付近に台風がある場合に不定期に運用される台風モデル（水平分解能24kmの領域モデルがベース）などがある。全球アンサンブル予報モデルは、分解能を落とした全球スペクトルモデルがベースだが、全球速報解析を標準とし、これに観測誤差等の不確定性を織り込んだ（摂動を加えた）複数の初期値を用意し、予報を複数（週間予報では標準ランを含め25メンバー）実行する。これにより、初期場の不確定性に伴う誤差が予報時間とともに拡大することによる予報のばらつきや信頼性などを知ることができる。また予報集団の平均場は、統計的には標準ラン単独予報よりも精度が良くなることが知られている。
数値予報の結果は、観測データやそれに基づく解析場と比較して各種統計的スコアを計算することにより客観的に検証されている。全球モデルの予報成績は各国予報センター間で交換されており、予報成績を検証し他の予報センターの結果と比較することにより、モデルのくせや欠点などが明らかになり、初期値作成手法や物理過程などモデル改良の参考に用いられる。
４．データ同化
数値予報は、ある境界条件の下で支配方程式の時間発展を計算する初期値問題で、正確な予報のためには大気の初期状態を正確に決定することが重要である。地球温暖化などを研究するための気候モデルとの大きな違いがここにある。大気の初期状態把握のためには観測が必要だが、一般には観測は限られているので、前の時間の数値予報の予報値を第一推定値として、それを観測で修正して初期値を作る作業が行われる。観測データを数値予報に取り込む作業を「データ同化」、データ同化によってモデルの初期時間の場を推定する作業を「解析」という。解析された初期場（解析場）には数値モデルの予報対象にはならないような時空間スケールの現象（「ノイズ」）が含まれていることがあり、モデルによる時間積分を始める前に、解析場からあらかじめノイズを取り除いたり、より予報に適した場に修正することがあり、「初期値化」と呼んでいる。初期場から数値予報を行った予報場は次の解析の第一推定値（解析のベースとなる場、「背景場」と呼ぶことがある）に再び使われる。解析−予報−解析−予報と連なるサイクルを解析予報サイクルという。
気象庁の数値予報に用いられる観測データとしては、地上観測、船舶、航空機、ブイ、高層ラジオゾンデなどの直接観測のほかに、衛星によって推定された風や気温、水蒸気のデータ、ウインドプロファイラ[6]による風のデータなどがある。RSM, MSMに関しては、レーダー・アメダス解析雨量のデータも使われるようになっている。これらの観測データには、測器の測定精度や空間代表性に起因する誤差の他に、人為的なミスや機器の故障に起因する誤りが含まれることがあり、このようなデータが混入すると解析場（と予報）の品質が大きく低下する。このような誤データを除去するために、データ同化処理の前段階として、観測データの品質管理を行っている。品質管理では、観測値の気候学的な整合性、第一推定値との差、周囲の観測値との整合性など様々なチェックが行われる。
解析値の作成には、これまでは最適内挿法と呼ばれる手法が広く用いられてきた。最適内挿法では、
解析値＝第一推定値＋修正値
の形式で、第一推定値を修正する。修正値は、周辺の観測値の第一推定値との差を修正係数（重み）で内挿して求める。修正係数は、観測誤差と予報誤差の大きさとその空間相関を用いて、修正値と観測値・第一推定値との規格化した距離が小さくなるように（条件付確率密度関数が最も大きくなるように）決める。
最適内挿法は手法が簡便であるが、解析変数と線形関係にある物理量しか同化できない、という制約があるため、最近では変分法と呼ばれるより高度な同化手法が使われるようになってきている。変分法の手法には、３次元変分法と４次元変分法がある。
３次元変分法では、以下のように定義されたコスト関数を最小化することによって解析値xを求める。
ここで、
は第一推定値、
は観測値、
はモデルの予報変数を観測物理量に変換する演算子(観測演算子と呼ぶ)である。
はそれぞれ背景誤差共分散行列(第一推定値の誤差とその空間相関)、観測誤差共分散行列(観測誤差とその空間相関)である。上式で、右辺第１項は解析値と第一推定値との差で背景項と呼ばれ、第２項は観測演算子によって変換された値と観測値との差で観測項と呼ばれる。Jcはペナルティ項で、内部重力波など解析値に含まれて欲しくないような気象学的ノイズを解析場から減らすための項である。３次元変分法では、観測演算子を導入することにより、解析変数と非線形な関係の物理量の観測データでも同化して情報を引き出すことができる。気象庁では、2001年10月から全球モデルの初期値作成にそれまでの最適内挿法に変わって３次元変分法を導入している。
４次元変分法では、以下のように定義されたコスト関数を最小化することによって解析値を求める。
３次元変分法との違いは、数値モデルの時間発展を表すモデル演算子Mが加わっていることで、評価関数は解析時間のみだけではなく、時間的広がりをもった同化期間（同化ウインドウ）全体で計算される。これによって、解析時刻の観測データでなくても、同化ウインドウに含まれる非定次時の観測データを生かすことができる（図１）。このことは、ウィンドプロファイラなどの高頻度の観測データの有効活用に大きな利点となる。また、評価関数にモデル演算子が含まれることにより、求められる解析値は物理的にバランスが取れたものになる。４次元変分法では、評価関数を最小化するため、アジョイントモデルといわれる評価関数の勾配を計算するための数値モデルが新たに必要になり、また繰り返し計算が必要なため多くの計算機資源も必要とする。
気象庁では、2002年3月から、MSMの初期値作成に４次元変分法（メソ４次元変分法）を導入している。これは境界条件を必要とする領域・局地モデルでは世界で最初の現業化である。図２は2002年５月15日06-09
UTCの降水の実況と予報で、左上に実況（レーダーアメダス解析雨量）を示す。同時刻を対象とするRSMも予報（右上）では降水は弱くしか表現されておらず、位置もずれている。一方、メソ４次元変分法による初期値を用いたMSM（左下）では、観測された雨域が比較的良く表現されている。気象庁では、今後RSMと全球モデルGSMの解析についても順次４次元変分法を導入していく計画である。変分法データ同化の詳細については、露木(1997)3)を、また、メソ四次元変分法実装方法の詳細については石川・小泉(2002)4)を参照して頂きたい。
５．非静力学モデル
前述した静力学近似は、100km以上の水平スケールの現象を予報対象にする場合には比較的高い精度で成り立つことから、気象庁GSM,RSM,MSMをはじめ、各国の殆どの数値予報モデルで用いられている。静力学モデルでは、予報対象とする現象のスケールと用いられる格子間隔の関係から、積雲対流などは格子スケール以下の現象としてパラメタライズされるのが普通である。
一方、集中豪雨などの顕著な降水現象の多くは、積乱雲やメソ対流系擾乱と呼ばれる積乱雲の集合体によって引き起こされる。これらの現象の水平スケールは通常数十km以下で、静力学近似が必ずしも十分な精度では成り立たない。また、水の相変化に伴う潜熱の解放と雲内水物質の分布が、運動場と降水域の決定に重要な役割を果たしている。従って、顕著な降水現象の予報には、雲の微物理過程を含む水平分解能５km以下の非静力学モデルを用いることが本質的に望ましい。また局地的な地形の影響を受ける風も、非静力学モデルの方が正しく表現することができる。非静力学モデルでは、水平分解能に原理的な制約がなくなるが、鉛直風と３次元の気圧を予報するために計算が複雑になる。このため、かつては対流など小スケールの現象理解のための研究用の道具としての利用が主だったが、近年の計算機能力の向上とモデルの改良により、天気予報への応用が始まりつつある。非静力学モデルについての詳細は日本気象学会から気象研究ノート(1999)
5)が発刊されている。
気象庁では、平成15年度を目途に現行MSMに代わる非静力学メソ数値予報モデル（NHM）を運用する計画で、そのための開発を行っている6)。NHMは、気象庁気象研究所と気象庁数値予報課が共同開発した非静力学モデル「MRI/NPD-NHM」7)をベースとして、数値予報課が中心になって10ｋｍ分解能での現業運用を想定して改良を加えているモデルである。降水過程としては、水物質を水蒸気、雲水、雲氷、雨、雪、あられの６つのカテゴリーに分けて、それらの混合比などを予報するバルク法の雲物理過程を含んでいる。NHMの主な仕様については表１に記してある。ベースとなったMRI/NPD-NHMの詳細は気象研究所ホームページ
(http://www.mri-jma.go.jp/Dep/fo/ mrinpd/INDEXJ.htm)からも閲覧することが出来る。
非静力学モデルの本来の性能を引き出すためには、出来るだけ高分解能にすることが望ましいが、MSM程度の領域を2-3km以下の分解能でカバーするには非常に大きな計算資源が必要となる。MSMは大雨の予想などを主目的としているために速報性が要求され、データの集信、解析からモデル計算、結果の配信までを限られた時間内に計算を終える必要がある。このため、現時点での計画では、基本的にMSM程度の領域をほぼ同等な分解能（水平約10km）で覆う予定である。10km分解能のモデルが表現する現象は数十km以上の水平スケールを持つので、非静力学の効果はそれ程大きくないと思われるが、降水過程に氷相を含む雲物理過程を含めることにより降水の表現には違いが出てくる場合がある。現業NHMでは初期値にMSM同様、メソ4次元変分法による解析を用いる予定である。メソ4次元変分法ではモデル演算子としてMSMをベースとした静力学スペクトルモデルを用いており、非静力学モデルとの相性に問題がないかも調べる必要がある。図２の右下には、2002年5月15日のメソ4次元変分法による初期値を用いた場合のNHMの予報例を示す。MSMでは九州東部や四国西部の降水が実況と比較して強過ぎるが、この例ではNHMはこれらについて改善している。
NHMは現業天気予報のみならず、小スケール現象の研究用にも適用可能なように設計されている。部外研究者にモデルを利用してもらうことは研究成果の還元を求めることにより新たな知見を得ることができ、モデル開発にとって大きなメリットとなることから、気象庁では平成12年度から積極的にモデルを貸与する方針をとっている。2002年7月からは気象庁の数値予報研究開発プラットフォームのホームページ
(http://pfi.kishou.go.jp/) を通じてモデルの利用申請からソースコード、実行スクリプトの取得までがオンラインで行えるようになっており、国内の大学・国立研究機関など、利用・開発コミュニティが拡がりつつある。
６．おわりに
現代の数値予報システムは、データの集信、デコード、品質管理、データ同化、数値積分による予報、予報結果からの応用プロダクトの作成・配信、に至る一貫した処理を短時間で安定に行わなければならず、全体で複雑かつ巨大なシステムとなっている。数十人規模のモデラーや技術者がチームワークを組んで構築する国家的科学技術であり、数値予報モデルを自主開発し数値解析予報システムを現業運用していくだけの能力を有している国は世界でも限られている。３章でも述べたように、モデルの予報結果や成績は各国予報センター間で交換されており、厳しい国際競争にさらされている。その一方で、国連の下部機関世界気象機構（ＷＭＯ）では、数値予報に関連するワーキンググループ活動や様々な国際研究プログラムを推進しており、各国の予報センター・研究機関・大学を通じて活発な技術交流が行われている。気象は数理モデルの応用対象として最も長い歴史を持つとともに、今後も地球シミュレータに代表されるような最大級の計算技術の応用対象であり続けると思われる。
謝辞 本稿執筆と図の利用に関して、郷田治稔、小泉耕、石田純一の各位をはじめとする気象庁数値予報課のスタッフにお世話になりました。
参考文献
1) 増田善信: 数値予報, 気象学のプロムナード３,
東京堂出版, 278pp (1981).
2) 時岡達志・山岬正紀・佐藤信夫: 気象の数値シミュレーション,
東京大学出版会, 247pp (1993).
3) 露木義: 変分法によるデータ同化,
数値予報課報告別冊, 気象庁予報部, 43, 102/165, (1997).
4) 石川宜広, 小泉耕: メソ4次元変分法,
数値予報課報告別冊, 気象庁予報部, 48, 37/59, (2002).
5) 斉藤和雄・小倉義光・吉崎正憲・村上正隆・川野哲也・山田哲司・里村雄彦・栗原和夫・加藤輝之: 非静力学モデル, 気象研究ノート, 日本気象学会, 196, 195pp (1999).
6) 石田純一, 斉藤和雄, 山田芳則,
藤田司, 成田正巳, 後藤進, 室井ちあし, 加藤輝之, 永戸久喜: 現業化に向けた気象庁非静力学メソモデルの開発について, 2002年度春季大会講演予稿集,
日本気象学会, 96, (2002).
7) K. Saito, T. Kato, H. Eito, and C. Muroi: Documentation of the
Meteorological Research Institute / Numerical Prediction Division unified nonhydrostatic
model. Tech. Rep. MRI, 41, 133pp (2001).
表１ 気象庁の代表的な数値予報モデル（NHMは開発中のモデル）
|
|
全球モデル (GSM) |
領域モデル (RSM) |
メソスケールモデル(MSM) |
非静力学モデル (NHM) |
|
予報領域 |
地球全体 |
東アジア 約6500km×5120km |
日本とその周辺 約3600km×約2880km |
同左 |
|
水平分解能 |
約60km (0.5625度) |
約20km |
約10km |
|
|
鉛直層数 |
40 |
40 |
40 |
|
|
予報時間 |
216時間1 |
51時間 |
18時間 |
|
|
初期時刻 |
00、12
UTC |
00、12
UTC |
00、06、12、18
UTC |
|
|
データ収集時間 |
約2.5時間 |
約3時間 |
約50分 |
|
|
解析 |
3次元変分法 |
3次元最適内挿法2 |
メソ4次元変分法 |
|
|
側面境界条件 |
なし |
同時刻のGSM |
直前のRSM |
|
|
支配方程式 |
静力学近似プリミティブ方程式 |
同左 |
非静力学方程式 |
|
|
予報変数 |
渦度、発散、地表気圧、温度、水蒸気、雲水 |
水平風、地表対数気圧、仮温度、水蒸気、 雲水（RSMのみ、予定） |
運動量、気圧、温位、乱流エネルギー、水蒸気、雲水、雲氷、雨、雪、あられ |
|
|
投影法 |
球面座標 |
等角投影（ランベルト） |
同左 |
|
|
鉛直座標 |
地形に沿った気圧座標系(σ-pハイブリッド座標) |
同左 |
地形に沿った高度座標系（z*座標） |
|
|
モデル上端 |
0.4 hPa |
10 hPa |
22 km |
|
|
水平差分 |
球面調和関数スペクトル法 |
二重フーリエ展開スペクトル法 |
フラックス型有限差分＋フラックスコレクション、 |
|
|
水平格子配置 |
(Arakawa -Aに相当) |
(Arakawa -Aに相当) |
Arakawa -C |
|
|
重力波 |
セミインプリシット |
同左 |
タイムスプリット |
|
|
音波 |
静力学近似による除去 |
同左 |
鉛直インプリシット 水平タイムスプリットに発散フィルターを併用 |
|
|
降水過程 |
大規模凝結＋湿潤対流調節＋Arakawa Schubert |
同左 |
雲水・雲氷・雨・雪・あられの混合比を予報＋氷相を考慮した対流調節 |
|
|
乱流・拡散 |
レベル２モデル |
レベル２モデル ノンローカル境界層 |
レベル2.5モデル |
|
（100UTCは90時間
22003年3月に４次元変分法に移行予定）
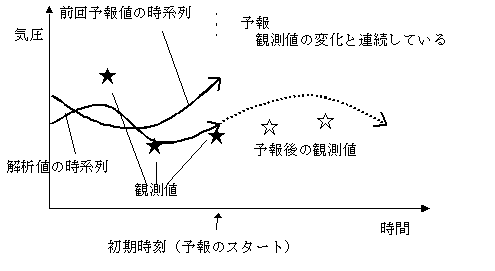
図１ 4次元変分法の模式図。
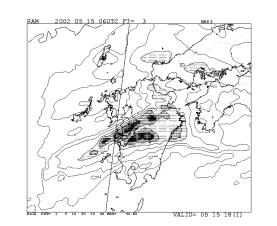
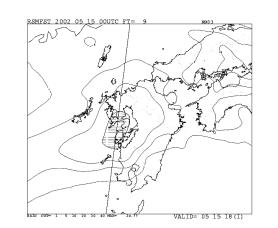
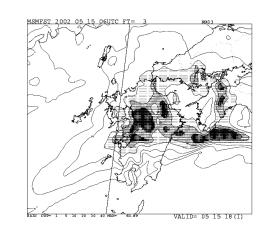
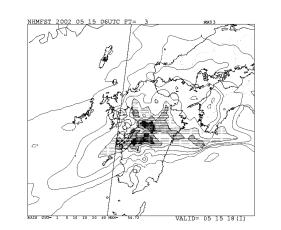
図２ 2002年５月15日06-09 UTCの降水の実況と予報。左上）レーダーアメダス解析雨量。
右上）５月15日00 UTC初期値のRSMの予報。左下）５月15日06 UTCのメソ４次元変分法による初期値を用いたMSMの予報。右下）同じく、NHMの予報。